La mano più pazza delle WSOP: AA vs KK vs QQ vs JJ!

La notizia ci arrivava direttamente dall’account di Twitter del giocatore Amit Makhija, che ha visto al suo tavolo una delle mani più improbabili che si possano dare a un tavolo da poker. Siamo al Day1C del Main Event delle WSOP 2013 e nessuno dei giocatori credeva ai propri occhi.

I  rilanci partivano senza sosta e alla fine tre giocatori andavano allo showdown, fiduciosi tutti che almeno uno degli altri due avversari avesse in mano AK, il che rafforzerebbe tantissmo la forza della propria mano. Invece no. Ognuno dei tre giocatori ha sfoderato una delle tre pocket pair più forti del mazzo: AA, KK e QQ. Le sorprese non sono finite qui, poiché il quarto giocatore coinvolto nella mano e che finalmente ha foldato sentendo puzza di bruciato ha dichiarato di aver foldato JJ.

Il risultato della mano? Assurdo. Non solo perché alla fine a vincere è stata la mano più debole, QQ, ma soprattutto perché sul board sono apparse i due jacks rimanenti, il che avrebbe fatto fare poker all’unico giocatore che è stato in grado di mollare la sua coppia. Il vero risultato? Un monster tilt per tutti i giocatori al tavolo (tranne per quello con QQ, si intende), anche se nessuno è stato eliminato.

Just saw AA vs QQ vs KK vs JJ. All found a way to get it in except for JJ. JJ woulda made Quads. QQ wins, no one busts everyones tilted.

— Amit Makhija (@amak316) July 8, 2013

Veniamo per un attimo alla parte matematica della mano. Che probabilità ci sono di vedere nella stessa mano queste quattro coppie una contro l’altra? Iniziamo per il calcolo più conosciuto: le probabilità di ricevere dal dealer una coppia di assi sono (4/52)*(3/51) = 0,00452172, ovvero una volta su 221 mani. È facile arrivarci: ci sono 4 assi in un mazzo di 52 carte e una volta che ne abbiamo estratto uno, ne rimangono 3 in un mazzo di 51 carte. Se continuiamo quella progressione, dobbiamo fare questo calcolo:

(4/52)*(3/51)*(4/50)*(3/49)*(4/48)*(3/47)*(4/46)*(3/45) = 0,00000000068292972
1 /0,00000000068292972 = 1.464.279.516,1997050003915483426318

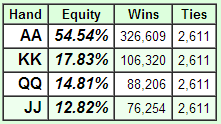
Morale: una mano del genere capita una sola volta ogni quasi un miliardo e mezzo di mani. Andiamo oltre. Quante mani dovremo vedere perché JJ vinca in questo spot? Bisogna prima capire qual è l’equity di JJ contro AA, KK e QQ. Inserendo queste mani su un simulatore otteniamo questi dati:

Ora basta molteplicare le probabilità che capiti quella mano per la probabilità che vinca JJ:

0,00000000068292972 * 0,1282 = 0,000000000087551590104

1 / 0,000000000087551590104 = 11.421.837.099,841692670760907508828

Da questo calcolo risulta che per vedere uno spot come quello dove a vincere sia la coppia di jacks dovremo aspettare più di 11 miliardi di mani. Bene, una è appena successa, sediamoci e ordiniamo qualcosa da bere perché l’attesa sarà lunga…